Перейти к:
Основные принципы расчета необходимой численности участников клинических исследований. Часть 2. Анализ выживаемости (обзор)
https://doi.org/10.30895/1991-2919-2025-15-1-92-104
Резюме
ВВЕДЕНИЕ. Анализ выживаемости — метод биостатистики, используемый в клинических исследованиях для подтверждения эффективности и безопасности применения лекарственных средств в долгосрочной перспективе. Актуальность метода определяется оценкой возможности экстраполяции заключения о полезности медицинского вмешательства, установленного в краткосрочном клиническом исследовании, на долгосрочный период наблюдения, а также возможности коррекции режимов дозирования и схем лечения. В настоящее время отсутствуют подробные методические рекомендации по проведению исследований по анализу выживаемости.
ЦЕЛЬ. Систематизация технических требований к планированию дизайна событийного исследования в части определения размера выборки.
ОБСУЖДЕНИЕ. Обсуждены методы расчета необходимой численности субъектов для анализа выживаемости в рамках событийных исследований, в которых сбор и оценка исходов проводится в условиях цензурирования наблюдений. Описаны вероятностные модели, построенные на основе байесовской теории вероятностей, для оценки параметров выживаемости, характеризующих время и риск наступления события, а также кумулятивную долю выживших, как основных переменных для определения размера выборки участников исследования. Рассмотрены теоретические основы анализа событийного риска в дизайнах исследования выживаемости. Представлено описание гипотез, статистических моделей расчета размера выборки субъектов, определения пороговых значений параметров выживаемости в групповых последовательных дизайнах исследования событийного риска.
ВЫВОДЫ. Представленные статистические модели могут использоваться при разработке дизайнов исследований, направленных на оценку продолжительности времени до момента наступления ожидаемого события и кумулятивного риска во время лечения и после применения лекарственных средств.
Ключевые слова
Для цитирования:
Шредер О.В., Горячев Д.В., Меркулов В.А. Основные принципы расчета необходимой численности участников клинических исследований. Часть 2. Анализ выживаемости (обзор). Регуляторные исследования и экспертиза лекарственных средств. 2025;15(1):92-104. https://doi.org/10.30895/1991-2919-2025-15-1-92-104
For citation:
Shreder O.V., Goryachev D.V., Merkulov V.A. Basic Principles for Calculating the Required Number of Participants in Clinical Trials. Part 2. Survival Analysis (Review). Regulatory Research and Medicine Evaluation. 2025;15(1):92-104. (In Russ.) https://doi.org/10.30895/1991-2919-2025-15-1-92-104
ВВЕДЕНИЕ
Планирование клинического исследования (КИ) требует четкой формулировки целей в определении клинически важных вопросов и способов их решения с учетом основных требований к репрезентативности выборочных совокупностей участников испытаний. Формат последующего статистического анализа определяется типом планируемого дизайна и исследовательских задач [1]. Большинство регистрационных исследований лекарственных средств (ЛС) являются проспективными, имеющими четко определенные визиты начала и завершения исследования для оценки терапевтического эффекта ЛС за определенный период лечения и постнаблюдения участников КИ (пациентов). Реже используют ретроспективный дизайн на основе изучения архивных данных ранее исследованных пациентов.
Дизайны проспективных и ретроспективных исследований в большинстве случаев разрабатываются на основе признанных регуляторами статистических моделей, предназначенных для подтверждения превосходства, не меньшей эффективности и эквивалентности новых терапевтических препаратов относительно референтного препарата или плацебо [2][3]. Однако указанные статистические модели не всегда применимы в случаях решения исследовательских задач в концепции событийного анализа рисков, возникающих в течение определенного периода времени наблюдения за пациентами, оценки отношения рисков и шансов развития интересующего события или прогноза исхода заболеваний при долгосрочном вмешательстве или необходимости последующего наблюдения после лечения [4][5]. В этом случае могут быть использованы вероятностные модели Байеса, позволяющие на основе моделирования условных и безусловных предположений, определяемых как априорная и апостериорная вероятность, прогнозировать наступление интересующих исследователя событий, связанных с риском применения ЛС, а также рассчитывать мощность и объем выборки участников для различных дизайнов последовательных групповых схем лечения.
Сложность планирования дизайнов событийных исследований обусловлена тем, что для анализа событийных параметров, например выживаемости, неприменимы стандартные модели, основанные на сравнении долей и средних величин. Для прогнозирования наступления интересующих событий в некоторый момент времени наблюдения наряду с количественными методами необходимо использовать логические модели.
Оценка размера выборки для событийных наблюдений является важной частью планирования, особенно в групповых последовательных дизайнах исследования выживания, связанных с цензурированием данных и определением времени интересующих исследователя исходов. В этом смысле метод анализа выживаемости является незаменимым инструментом в исследованиях с долгосрочным вмешательством, которое сопровождается значительной частотой выбывания пациентов из исследования по причине исключения, нежелательных явлений, случаев смерти или других причин.
Цель работы — систематизация технических требований к планированию дизайна событийного исследования в части определения размера выборки.
ОСНОВНАЯ ЧАСТЬ
При формулировке научных гипотез оценки риска медицинского вмешательства в долгосрочной перспективе используются модели вероятностной статистики, основывающиеся, как правило, на положениях теоремы Байеса1 [1]. Базовая формула теории вероятности, согласно теореме Байеса, имеет вид (1):
P(A|B) = P(B|A) × P(A) ⁄ Р(B), (1)
где P(A|B) — апостериорная вероятность2 гипотезы А (условная вероятность), P(A) | Р(B) — априорная вероятность3 (безусловная вероятность), P(A) — вероятность априорных предположений, P(B|A) — вероятность правдоподобия4 (условная вероятность), Р(B) — данные, нормализующие5 апостериорную вероятность, А — предположения (гипотезы), В — известные данные (события) [4–8]. Согласно теореме Байеса при априорных предположениях можно определить вероятность наступления ожидаемого события в планируемом исследовании, выраженную в коэффициентах риска, то есть посредством отношения как средних (медианных), так и процентных (долевых) значений [9–14].
Вероятности правдоподобия определяются для каждой сформулированной гипотезы, затем по уравнению (1) можно пересчитать вероятности на основе данных, полученных в эксперименте, (2) [15].
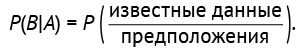 (2)
(2)
Необходимость четкого описания статистических дизайнов, основным критерием которых является оценка риска, предполагает более подробное пояснение к модификации базовой модели Байеса, в частности, это касается формулировки гипотез и выбора методов оценки клинических исходов, таких как функция выживаемости, функция риска, часто выражающая соотношения рисков и шансов ответа на медицинское вмешательство, и кумулятивная выживаемость участников исследования.
Метод анализа выживаемости
Выживаемость — это вероятность пережить любой из моментов времени после некоторого начального события, которая задается кривой выживаемости, определяющей долю выживших к моменту времени t от начала наблюдения t0. Метод анализа выживаемости используется в клинических дизайнах, направленных на оценку продолжительности периода до наступления события, интересующего исследователя. Этот метод основан на анализе функции выживаемости6, которая определяет вероятность наступления события в конкретный момент времени и вероятность выживания пациентов с течением времени [2][15][16]. За событие может быть принята как смерть пациента, так и любое другое событие: успешное излечение, исчезновение целевых симптомов заболевания, преждевременное прекращение лечения, развитие/регрессия нежелательных реакций, частотные переменные, характеризующие количество пациентов в динамике по времени излечения, рецидива или выбывания из наблюдения по разным причинам в определенные интервалы времени лечения или постнаблюдения и др.
Метод анализа выживаемости получил широкое распространение в исследованиях кардиологии [16] и онкологии [17], однако этот метод может успешно применяться в оценке любых терапевтических эффектов, диагностических критериев и исходов целого ряда заболеваний, при которых основным критерием оценки эффекта является временной фактор [16–18].
В основе анализа выживаемости лежит метод Каплана–Мейера, позволяющий определить время выживания (продолжительности события) от определенной даты начала (например, включения пациентов в исследование) до момента исхода события (времени излечения, рецидива, смерти, выбывания из исследования или другого значимого события). Такая оценка реализуется посредством расчета продолжительности времени с учетом цензурированных7 наблюдаемых событий или участников исследования.
График оценки Каплана–Мейера представляет собой визуализацию функции выживаемости в виде ломаных линий — горизонтальных ступеней, отражающих временные интервалы вероятности наступления события, которая рассчитывается по формуле (1), модифицированной относительно исследовательской задачи определения вероятности риска выбывания пациентов из исследования в интервале определенного времени наблюдения, и имеет вид (3):
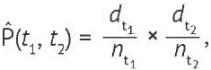 (3)
(3)
где dt1 и dt2 — абсолютное число (или доля) пациентов, умерших в интервале времени t1 и t2 соответственно, nt1 и nt2 — общее число наблюдаемых пациентов в интервале времени t1 и t2, и Р̂(t1, t2) — вероятность риска выбывания из исследования в интервале времени t1 и t2 [15–19].
В контексте вероятности выживания участников исследования Р̂(t1, t2) может выражаться формулой (4):
Р̂(t1, t2) = Р(t1) ∙ Р(t2), (4)
где 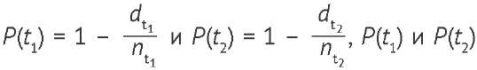 — вероятность риска выбывания из исследования в интервале времени t1 и t2, соответственно.
— вероятность риска выбывания из исследования в интервале времени t1 и t2, соответственно.
Целью анализа в данном случае является оценка вероятности выживания участников исследования с учетом риска выбывания части пациентов по разным причинам (или наступление целевого события) в определенные интервалы времени (до наступления момента времени t1 или t2).
Таким образом, для определенного интервала времени, в котором зарегистрировано целевое событие, оценивают вероятность пережить этот интервал времени как отношение числа выбывших (умерших) пациентов (dt) к числу наблюдавшихся в момент времени наблюдения (nt). Фактически отношение dt к nt является показателем риска выбытия (смерти) из исследования, а для определения вероятности выживания пациентов используют выражение 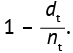 . Вероятность для каждого участника исследования пережить несколько интервалов времени будет равна произведению этих оценок от нулевого (t0) до заданного момента (t1 и t2), в соответствии с правилом умножения вероятностей [2][15][16]. Например, если все пациенты начали наблюдаться в момент времени t0, расчет длительности наблюдения и регистрация целевых событий (летальный исход или выбывание по другой причине) производится до определенных моментов времени (t1 и t2).
. Вероятность для каждого участника исследования пережить несколько интервалов времени будет равна произведению этих оценок от нулевого (t0) до заданного момента (t1 и t2), в соответствии с правилом умножения вероятностей [2][15][16]. Например, если все пациенты начали наблюдаться в момент времени t0, расчет длительности наблюдения и регистрация целевых событий (летальный исход или выбывание по другой причине) производится до определенных моментов времени (t1 и t2).
Результатом анализа является интервал времени от начала наблюдения до наступления определенного события, часто называемый временем анализа выживаемости. Пациентов, у которых не зарегистрировано событие (или выживших) на момент анализа данных, отмечают как цензурированных8 знаком «+». При анализе таких данных используется информация от всех участников исследования: тех, у кого событие наступило к концу исследования, и тех, у кого не наступило. Однако выводы о выживаемости участников основываются на времени наступления события и, следовательно, зависят от количества событий, наблюдаемых в исследовании.
Общая выживаемость участников исследования может быть представлена в виде формулы Каплана–Мейера для всех временных интервалов t, в которых были зарегистрированы случаи летальных исходов (5):
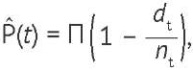 (5)
(5)
где Р̂(t) — общая выживаемость, dt — число умерших в интервале времени t, nt — число пациентов, наблюдавшихся в интервале времени t, П — символ произведения значений  для всех временных интервалов, в которых были зарегистрированы случаи выбывания (смерти) пациентов.
для всех временных интервалов, в которых были зарегистрированы случаи выбывания (смерти) пациентов.
Рассмотрим пример расчета выживаемости методом Каплана–Мейера. Предположим, что из 10 включенных в исследование пациентов один умер через 2 месяца, один — через 6 месяцев, двое — через 7 месяцев после начала наблюдения. Вероятность умереть через 2 месяца составит  вероятность выжить через 2 месяца для пациентов, которые дожили до этого времени:
вероятность выжить через 2 месяца для пациентов, которые дожили до этого времени:  Вероятность выжить через 6 месяцев для пациентов, которые дожили до этого времени:
Вероятность выжить через 6 месяцев для пациентов, которые дожили до этого времени:  Вероятность выжить через 7 месяцев для пациентов, которые дожили до этого времени:
Вероятность выжить через 7 месяцев для пациентов, которые дожили до этого времени: 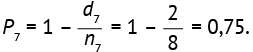 Таким образом, Р̂ (выживаемость в интервале времени t2, t6 и t7) = Р2 × Р6 × Р7 = 0,900×0,889×0,750 = 0,600.
Таким образом, Р̂ (выживаемость в интервале времени t2, t6 и t7) = Р2 × Р6 × Р7 = 0,900×0,889×0,750 = 0,600.
Следует отметить, что формула (5) выражает вероятность выживаемости пациентов до определенного момента времени t, рассчитанную на основе интенсивности наступления событий (летальных исходов) или функции риска, обратной оценкой которой является функция выживаемости S(t), связанная с Р̂(t) соотношением (6) [16]:
Р̂(t) = 1 – S(t), (6)
где S(t) является отношением числа выживших в интервале времени t к общему числу наблюдавшихся пациентов и определяется формулой (7).
В дизайне событийного исследования наиболее часто используемыми параметрами оценки являются функция выживаемости (дожития), функция риска (интенсивности наступления событий) и кумулятивная доля выживших [16–19].
Функция выживаемости Ŝ(t) — вероятность выживания до момента времени t, Ŝ(t) = P(T > t), где T — случайная величина времени до наступления целевого события и определяется формулой (7).
 (7)
(7)
где значения Ŝ(t) могут быть в диапазоне от 0 до 1.
Пример: если из 10 наблюдаемых в течение 3 лет выжили 6 пациентов, то вероятность выживания пациента в течение 3 лет после лечения равна S(t)=6/10=0,6.
Функция риска или интенсивности наступления событий F(t) — используется для прогнозирования риска наступления событий в будущем и определяется как оценка вероятности наступления целевого события в заданный момент времени, притом что это событие не наступило ранее в начальном интервале времени:
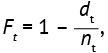
где, dt — число целевых событий (выбытий, случаев смерти) в заданный интервал времени t, nt — число участников исследования, доживших до момента времени, находящегося в интервале t.
Функция риска является обратной функции выживаемости, она может быть представлена коэффициентом риска (HR), выраженным отношением долей S1 и S2 или другими соотношениями, например отношением логарифмов частотных показателей (8), отношением коэффициентов показателей выживаемости (9) и медианных значений (10, 11) в зависимости от метрических характеристик исследуемых параметров выживаемости. Формула расчета HR на основе отношения логарифмов выживаемости S1 и S2 имеет вид (8):
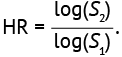 (8)
(8)
Если целевым событием является рецидив заболевания, то распределение случаев выживания (выздоровления) для каждого вида лечения можно представить в виде показателя частоты, а коэффициенты риска (λ1 и λ2) рассчитываются как отношение частот случаев рецидива и выздоровления для каждой из групп лечения за определенный промежуток времени, однако при сравнении двух методов лечения показатель «коэффициент риска рецидивов» HR будет рассматриваться как отношение долей λ1 и λ2 , выраженных в диапазоне значений от 0 до 1 (9),
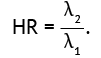 (9)
(9)
Это выражение, описывающее отношение в долях, сродни вычислению различий значений в виде λ1−λ2 [1], которое используется при выполнении логрангового теста для сравнения двух групп лечения, но в данном случае коэффициент риска HR определяется экспоненциальным распределением не преобразованных данных λ, оценивается с использованием методов максимального правдоподобия9 и рассчитывается путем деления показателя риска в группе лечения λ2 на показатель в контрольной группе λ1 при условии, что лечение, которое дает лучшие результаты, чем в контрольной группе, будет иметь коэффициент риска меньше единицы.
При планировании исследования можно получить информацию об ожидаемой доле выживших на основе значений контрольной и экспериментальной групп, известных из предыдущих исследований. Если коэффициент риска постоянен во времени, его можно вычислить из отношения логарифмов выживаемости S1 или S2, используя уравнение (8) в модификации (10) [9][10][15].
Например, если выживаемость в течение 1 года при стандартном лечении составляет 0,2, а новый метод лечения увеличивает выживаемость до 0,3, то, согласно (9), HR будет равен 1,5, где разница (λ1−λ2 ), выраженная в процентном соотношении, покажет увеличение выживаемости при новом лечении на 50%.
Ожидаемый эффект лечения можно оценить, рассчитав требуемое минимальное значение HR, исходя из известного S1 для контрольной группы по уравнению (10):
S2 = exp{HR(log(S1))}. (10)
Например, если значение S1 равно 0,4, и показатель риска снижается на 50% (в диапазоне от 0 до 1 = 0,5), то этого достаточно для определения пользы режима лечения, как S2 = exp(log)(0.4)(0,5)) = 0,632.
Если коэффициент риска не меняется с течением времени, то он может быть выражен через медиану выживаемости (М1 и М2) по уравнению (11) [6–12].
 (11)
(11)
Медиана выживаемости для выборочной совокупности определяется как наименьшее время по кривой выживаемости, при котором выживаемость пациентов составляет меньше 0,5 (50%). Если число выбывших (умерших) пациентов составляет меньше половины наблюдаемой выборочной совокупности, медиану выживаемости определить невозможно. Если планируется оценка среднего значения параметра выживаемости, в качестве априорного можно использовать нормальное распределение данных, где среднее и дисперсия выбираются на основе известных, ранее изученных данных о параметре. Если планируется оценка доли выживших (успешных событий) на основе пропорций, то можно использовать бета-распределение10.
Кумулятивная доля выживших / функция кумулятивной выживаемости H(t) — это накопленная доля выживших в периоде от начала до окончания наблюдения. Функция кумулятивной выживаемости определяется в фиксированном интервале времени t0 как сумма вероятностей выживания до моментов времени t. Кумулятивная доля выживших определяется как события с известной интенсивностью (λ), то есть количеством событий, которые происходят независимо в фиксированном интервале времени t0 и описываются распределением Пуассона11 [15].
Коэффициент кумулятивного риска в данном случае определяется экспоненциальным распределением значений λ и оценивается с использованием оценок максимального правдоподобия. На этапе планирования необходимо получить оценку этого параметра, учитывая условие экспоненциального распределения в фиксированном интервале времени t0:
 (12)
(12)
где S(t) = e–λt, t ≥ 0 — вероятность выживания в течение t лет (функция распределения кумулятивной выживаемости).
Чтобы получить оценку λ, необходимо знать только долю выживших в течение фиксированного периода времени, в случаях отсутствия потерь при последующем наблюдении λ = 0.
Пояснить вышесказанное можно на следующем примере: если параметр фиксированного времени t0 равен 5 годам наблюдения, а доля выживших пациентов равна 0,7, то 70% пациентов выживают в течение не менее 5 лет.
Если известны доли пациентов в контрольной группе S1 и группе лечения S2, которые дожили до истечения t0, можно определить коэффициенты риска λ1 и λ2. Коэффициенты риска рассчитываются по формулам (13) [15][20].
 (13)
(13)
И, обратно, зная коэффициенты риска, можно рассчитать доли пациентов S1 и S2, доживших до момента t (14):
S1 = exp(–λ1t) и S2 = exp(–λ2t). (14)
Оценка коэффициента риска может быть получена на основе медианы продолжительности жизни, доли выживших после определенного периода времени наблюдения и отношения коэффициентов риска сравниваемых методов или групп исследования. HR для отношения рисков постоянных во времени в зависимости от исходных данных, условий и задач исследования аналогично (9) может иметь вид (15):
 (15)
(15)
где h1 и h2 — величина риска для контрольной группы и группы лечения.
Тестирование гипотез в дизайнах событийных исследований
В зависимости от цели планируемого исследования и типа данных (метрических характеристик переменных) в качестве инструмента выбора параметров выживаемости8 применяют различные статистические методы. Основными для решения исследовательских задач по оценке событийного риска по времени наблюдения для пациентов являются методы Каплана–Мейера, Нельсона–Аалена, Кокса, логранговый тест.
Метод Каплана–Мейера применяется для оп-ределения вероятности наступления целевого события в определенный интервал времени. Основным инструментом для определения количества выживших пациентов или частоты наступления событий по времени наблюдения является цензурирование, а результатом — кривая распределения функции выживаемости. Для описания частоты событий по времени наблюдения в группах исследования используют таблицы жизни, кривые Каплана–Мейера (рис. 1), функцию выживаемости S(t) и функцию кумулятивного риска, связанных отношением (6). Результаты оценки методом Каплана–Мейера могут быть представлены в виде кривой выживаемости, частоты наступления события в виде медианы или среднего значения, 95% доверительных интервалов показателей наступления событий, статистической значимости различий по показателю наступления событий в анализируемых выборках пациентов на основе критерия Вилкоксона и логранка (Мантела–Кокса) для учета различий в вероятностях события.
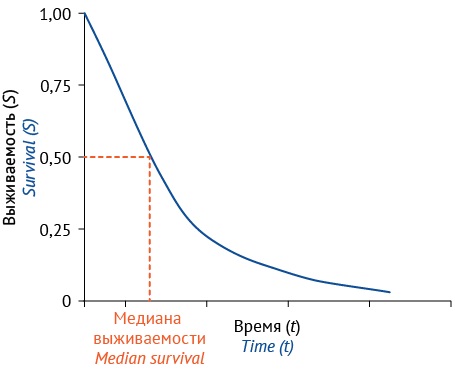
Рисунок подготовлен авторами / The figure is prepared by the authors
Рис. 1. Пример типичной кривой выживаемости
Fig. 1. An example of a typical survival curve
Кривая выживаемости (рис. 1) может применяться для описания продолжительности любых интересующих событий (процессов) [9][10][15][19]. В интервале значений [ 0; 1] на заданный момент времени (t0) наблюдения значение S(t) принимается равным 1 и в течение времени наблюдения стремится к нулю при указанном выше условии, что величина 0,5 является медианой выживаемости. Если в качестве исхода (события) будет выступать положительный ответ на лечение к некоторому моменту времени, то выживаемость S(t) определяется по формуле (7). Если задачей исследования является определение числа выживших (или другого интересующего события) за период наблюдения, включающий несколько временных интервалов, необходимо применить правило умножения вероятностей в соответствии с формулой (5).
Метод Нельсона–Аалена — альтернатива методу Каплана–Мейера; может применяться для оценки кумулятивного риска, определяемого как HR, описания влияния переменных на выживаемость, в частности, на основе данных о выживших и умерших участниках исследования для оценки функции выживаемости и функции риска летального исхода. Значения, рассчитанные на основе оценок Каплана–Мейера и Нельсона–Аалена, асимптотически эквивалентны при определении одних и тех же параметров и связаны отношением (16).
H(t) = –ln{S(t)}
и обратной функцией S(t) = exp{–H(t)}, (16)
где H(t) — кумулятивный риск, S(t) — выживаемость.
Метод Нельсона–Аалена базируется на теории случайных процессов, в частности, процессе Пуассона, описывающем независимость частоты событий в фиксированном интервале времени от числа событий, происходящих с постоянной интенсивностью в других непересекающихся интервалах времени, и подчиняется распределению Пуассона. В этом подходе для вычисления функции выживаемости и функции риска используется рекурсивное уравнение12, которое позволяет сравнивать степень риска для пациентов, например вероятности рецидива заболевания в какой-то момент времени у пациентов с разной степенью тяжести заболевания или альтернативными методами терапии [15][18–19].
Метод Кокса / модель пропорциональных рисков применяется для определения влияния некоторых факторов на вероятность выживания, например при оценке эффективности ЛС или прогнозировании выживаемости пациентов. Метод базируется на предположении о пропорциональности рисков, где основным инструментом является регрессионная модель Кокса для оценки влияния факторов риска наступления события (независимые переменные — предикторы) на показатели выживаемости пациентов, выраженные как функция от времени (время наступления события — функции риска) и в соответствии с основным правилом теории Байеса (1) определяет правдоподобие наступления события. В математическом выражении риск наступления события равен предельному значению условной вероятности (правдоподобию) наступления события P(В|А) в интервале времени (t, t + dt) для пациентов, находящихся в группе риска на момент времени t, деленному на длину временного интервала dt, где функция интенсивности наступления событий 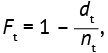 и в соответствии с логикой преобразований по (2) и (3) HR может быть рассчитан по формуле (5) [15][18–20]. В качестве основных параметров для прогнозирования риска наступления события и оценки влияния независимых переменных на этот риск используют логарифм отношения шансов (отношения вероятностей) и значения, объясняющие переменные (факторы). Пропорциональность рисков означает, что отношение шансов для двух сравниваемых групп не зависит от времени наблюдения, то есть влияние факторов на вероятность выживания не меняется со временем, при этом регрессия Кокса предполагает, что риск наступления события для i-го пациента имеет вид (17) [15][18]:
и в соответствии с логикой преобразований по (2) и (3) HR может быть рассчитан по формуле (5) [15][18–20]. В качестве основных параметров для прогнозирования риска наступления события и оценки влияния независимых переменных на этот риск используют логарифм отношения шансов (отношения вероятностей) и значения, объясняющие переменные (факторы). Пропорциональность рисков означает, что отношение шансов для двух сравниваемых групп не зависит от времени наблюдения, то есть влияние факторов на вероятность выживания не меняется со временем, при этом регрессия Кокса предполагает, что риск наступления события для i-го пациента имеет вид (17) [15][18]:
ln hi = ln h0(t) + β1 X1 + β2 X2 + ... + βpXp, (17)
где h0(t) — базовый риск, общий для всех пациентов; X1, ..., Xp — независимые переменные, предикторы; β1, ..., βp — коэффициенты регрессии, отражающие влияние предикторов на функцию риска [20]. При увеличении значения Xi и фиксированных значениях остальных предикторов риск наступления события возрастает в exp(βi) раз и в виде экспоненциальной модели выживаемости имеет вид [12][17]:
hi(t) = exp(α + β1 X1 + β2 X2 + ... + βp Xp) (18)
и с учетом базового риска:
hi(t) = h0(t) exp(α + β1 X1 + β2 X2 + ... + βp Xp). (19)
В соответствии с описанной моделью Кокса риск наступления события прямо пропорционален времени с учетом ковариат, зависящих от времени. Метод является полупараметрическим из предположения, что все переменные линейно влияют на логарифм функции риска (8) [21–23].
Логарифмический ранговый тест (логранговый тест) применяется для оценки значимости различий между исследуемыми группами по частоте событий в определенный (фиксированный) интервал времени путем сравнения времени выживания. Логранговый критерий определяет различия между группами лечения, критерий χ-квадрат определяет p-значение при условии значения альфа, равного 0,05 [1].
Логранговый критерий для сравнения кривых выживаемости используют при следующих допущениях:
- сравниваемые выборки участников (группы) являются случайными и независимыми;
- выбывание в интервале наблюдения одинаково в обеих группах;
- функции выживаемости в сравниваемых группах связаны соотношением (20):
S2(t) = [S1(t)]Ψ, (20)
где Ψ — отношение случаев смертей (событий). При Ψ = 1 кривые выживаемости совпадают, при Ψ < 1 участники 2 группы выбывают позже, чем в 1 группе, при Ψ > 1 участники 1 группы выбывают позже, чем в 2 группе [15].
Сравнение двух распределений выживаемости посредством логрангового критерия широко используется в событийных исследованиях и считается более эффективным, чем анализ, основанный на сравнении пропорций, поскольку позволяет сравнивать выживаемость в течение всего периода времени исследования, а не только в одной или двух временных точках наблюдения за пациентами. Используемые расчеты мощности предполагают экспоненциальное распределение времени выживания участников, что часто не совпадает с данными реальных клинических исследований. Тем не менее такое предположение является приемлемым, так как логарифмический ранговый тест и тест, полученный с использованием экспоненциального распределения, имеют практически одинаковую мощность в случае, если данные распределены экспоненциально. Кроме того, при использовании модели пропорциональных рисков (метод Кокса), когда данные представлены в виде соотношения рисков в соответствии с (9) и (11) и предполагается сравнение групп с помощью логрангового теста, распределение показателей выживаемости может быть преобразовано в экспоненциальное с учетом того, что условие применимости логрангового тестирования остается неизменным при монотонных преобразованиях13.
Таким образом, для сравнения указанных параметров выживаемости в двух и более группах исследования в большинстве случаев применяют логранговый критерий, а для оценки влияния различных факторов (категориальных или количественных переменных) на выживаемость — регрессию пропорциональных рисков Кокса. В качестве дополнительных статистических инструментов для оценки событийных исследований может применяться и ряд других критериев (табл. 1) в соответствии с целями планируемого исследования и оценочной шкалой целевых параметров выживаемости (конечных точек).
Таблица 1. Рекомендуемые статистические критерии для тестирования гипотез в дизайнах событийных исследований [15][18–21]
Table 1. Recommended statistics for testing hypotheses in event-based study designs [15][18–21]
|
Типы данных Data types |
Сравнение двух независимых выборок Comparison of two independent samples |
Сравнение более чем двух независимых выборок Comparison of more than two independent samples |
Сравнение двух зависимых выборок* Comparison of two dependent samples* |
Сравнение двух и более факторов воздействия в одной группе пациентов** Comparison of two or more factors in one group of patients** |
Оценка взаимосвязи между двумя показателями / явлениями Relationship between two estimated parameters/events |
|
Количественные (нормальное распределение) Quantitative (normal distribution) |
t-критерий Стьюдента Student’s t-test |
Дисперсионный анализ Analysis of variance |
Парный t-критерий Стьюдента Paired t-test |
Дисперсионный анализ повторных измерений Analysis of variance with repeated measurements |
Линейная регрессия, корреляция или метод Блэнда–Алтмана Linear regression, correlation, or Bland–Altman analysis |
|
Качественные (бинарные) Categorical (binary) |
Критерий χ² χ² test |
Критерий χ² χ² test |
Критерий Мак-Нимара McNemar’s test |
Критерий Кокрена Cochran’s test |
Коэффициент сопряженности Contingency coefficient |
|
Качественные (порядковые) Categorical (ordinal) |
Критерий Манна–Уитни Mann–Whitney test |
Критерий Крускала–Уоллиса Kruskal–Wallis test |
Критерий Вилкоксона Wilcoxon’s test |
Критерий Фридмана Friedman’s test |
Коэффициент ранговой корреляции Спирмена Spearman’s rank correlation coefficient |
|
Выживаемость Survival |
Критерий Гехана–Вилкоксона Gehan–Wilcoxon test |
Логранговый критерий (Мантела–Кокса) Log-rank (Mantel–Cox) test |
F-критерий Кокса и логранговый критерий Cox’s F-test, log-rank test |
Регрессионные модели Кокса (экспоненциальная, нормальная, логнормальная, пропорциональных рисков) Cox’s (exponential, normal, lognormal, proportional hazards) regression models |
Регрессионные модели Кокса (экспоненциальная, нормальная, логнормальная, пропорциональных рисков) Cox’s (exponential, normal, lognormal, proportional hazard) regression models |
Таблица составлена авторами на основании данных литературы / The table was prepared by the authors using literature data
* Например, одна группа пациентов до и после лечения. ** Например, несколько видов лечения.
* E.g., one group of patients before and after treatment. ** E.g., several treatments.
Во всех вышеописанных подходах к анализу данных событийных исследований необходимо придерживаться определенного порядка оценивания, представления целевых параметров выживания и их интерпретации.
Порядок выполнения анализа данных событийного исследования включает:
1) сбор данных о вероятности выживания, времени наблюдения, рисках и факторах (в случае анализа методом Кокса), которые могут оказать влияние на вероятность выживания;
2) проверку предположения о пропорциональности рисков с помощью графических методов, например посредством сравнения кривых Каплана–Майера для каждой группы;
3) проведение анализа методом, соответствующим цели исследования и типу данных целевых параметров (оценочной шкалы). Например, для оценки влияния факторов риска наступления события следует использовать метод Кокса с определением коэффициентов регрессии и их значимости или логранговый критерий для сравнения времени выживания с целью определения значимости различий между исследуемыми группами по частоте событий;
4) расчет 95% доверительных интервалов для целевых показателей выживаемости;
5) определение статистической значимости различий по показателю наступления событий в анализируемых выборках пациентов на основе критерия Вилкоксона и логранка (Мантела–Кокса);
6) представление 95% доверительных интервалов для отношения (6), (8) или разницы (7) показателей выживаемости групп сравнения;
7) интерпретацию результатов в контексте пропорциональности рисков или различий по параметрам выживаемости пациентов в группах исследования и тестовой статистики с подтверждением принятия или отклонения исследовательских гипотез нулевой H0 или альтернативной H1 на основе заданных клинически значимых пороговых значений. В процессе интерпретации данных рекомендуется представление графиков функций, определяемых как «выживание» (кумулятивная функция дожития в линейных координатах), «1 — выживание» (функция «1 — функция дожития» в линейных координатах), «риск» (функция накопленного риска в линейных координатах) и «логарифм отношения показателей выживания» (кумулятивная функция дожития в логарифмических координатах). Если используются факторные переменные, указанные графики выживания строятся для каждой из исследуемых групп (или выборок).
Определение размера выборки в дизайнах событийных исследований
Выбор формулы для определения размера выборки планируемого дизайна исследования производится с учетом метрических характеристик конечных точек и методов последующего тестирования исследовательских гипотез, условий их применимости и ограничений [20][21]. В рамках событийных исследований относительно конечных точек предполагается использование данных с нормальным или биномиальным распределением, определяемых в терминах событийного исследования как функция выживаемости, функция риска, кумулятивная доля выживших.
Исследовательская гипотеза может быть сформулирована в предположении о пропорциональных рисках, например коэффициента риска, который может быть получен на основе отношения медиан времени, долей целевых событий (смертность) или долей выживших до определенной (заданной) временной точки t [15].
Тестирование на основе нулевой (H0) и альтернативной (H1) гипотез о равенстве медианного времени выживания имеет вид: H0: Mт = Mc против H1: Mт ≠ Mc, где Mт и Mс — медианное время выживания для группы лечения и контрольной группы соответственно. В соответствии с предположением о пропорциональном риске гипотеза эквивалентности будет следующей: H0: θ=1 против H1: θ≠1, где θ — коэффициент риска = (MT/MC)y, где y — распределение Вейбулла. Размер выборки для планируемого исследования может быть рассчитан по формуле (21). Чем выше коэффициент риска при фиксированном значении y, тем меньше размер выборки участников исследования.
 (21)
(21)
где N — размер выборки. zα/2 и zβ — соответствующие значения стандартного нормального распределения.
Гипотеза о не меньшей эффективности может быть представлена в виде: H0: HR≥HR0 против H1: HR<HR0, где HR0 — максимальное значение коэффициента рисков, которое позволяет сделать вывод о не меньшей эффективности (эквивалентности). При нулевой гипотезе H0: HR=1. Для заданной границы не меньшей эффективности HR0>1 (максимальный коэффициент клинической незначимости) для отношения рисков постоянных во времени в соответствии с формулой (15).
Оценка коэффициента риска (HR) может быть получена исходя из значений медианы продолжительности жизни, коэффициента риска или доли выживших после определенного периода времени наблюдения. При расчете общего размера выборки могут быть использованы данные о числе событий или пациентов в зависимости от условий и задач исследования.
Пример. Если в качестве конечной точки предполагается получить данные с биномиальным распределением, то размер выборки может быть рассчитан на основе доли пациентов с интересующими исследователя целевыми событиями по формуле (22):
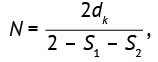 (22)
(22)
где S1 и S2 — коэффициенты выживаемости двух групп, dk — число целевых событий, N — общий объем выборки, который поровну делится между группами 1 и 2, то есть N/2.
Выражение (22) в преобразованном виде может использоваться для определения ожидаемого числа событий, которое рассчитывается на основе данных по количеству выживших, полученных в предыдущих исследованиях (или из данных литературы):
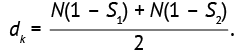 (23)
(23)
Процедура статистического планирования в части определения выборочной совокупности в этом случае включает:
1) определение границы принятия решения (пороговой величины) на основе заданной функции распределения и альфа-значения;
2) определение параметра смещения относительно пороговой величины и заданном значении мощности;
3) расчет числа событий для каждой группы dk в соответствии с выражением (23);
4) расчет размера выборки N по формуле (22) исходя из количества событий, рассчитанного по формуле (23).
Пример 2. Для дизайнов, основанных на сравнении кривых выживаемости двух групп пациентов посредством логрангового критерия [6–12], нулевую гипотезу формулируют в виде «в обеих группах выживаемость одинаковая» и учитывают ряд условий:
- две сравниваемые выборки независимы и случайны;
- выбывание в обеих выборках одинаково;
- функции выживаемости связаны соотношением (9), которое можно оценить как
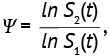 где S1(t) и S2(t) выживаемость в 1-й и 2-й группах в определенный период времени наблюдения t. Число целевых событий (например, смертей или рецидивов) предварительно рассчитывают по формуле (24):
где S1(t) и S2(t) выживаемость в 1-й и 2-й группах в определенный период времени наблюдения t. Число целевых событий (например, смертей или рецидивов) предварительно рассчитывают по формуле (24):
 (24)
(24)
где Ψ — отношение целевых событий (смертей или рецидивов), zα и z1–β — соответствующие значения стандартного нормального распределения [1].
Размер выборки участников для каждой из групп исследования может определяться по формуле (25):
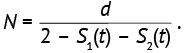 (25)
(25)
Пусть при новом лечении выживаемость пациентов должна повыситься с 30 до 60% (S1=30%, S2=60%). Тестирование для установления значимости различий с вероятностью 80% (z1–β=z0,80=0,84) планируется при уровне значимости 0,05 (zα=z0,05=1,96), отношение целевых событий составит:  Число целевых событий составит
Число целевых событий составит  48,1; тогда размер выборки для каждой из групп исследования составит
48,1; тогда размер выборки для каждой из групп исследования составит 
ЗАКЛЮЧЕНИЕ
Оценка эффективности медицинских вмешательств в долгосрочной перспективе и рисков, связанных с испытанием новых ЛС, в частности с выявлением нежелательных исходов в последующий после лечения период наблюдения на основе метода анализа выживаемости, позволяет скорректировать признание полезности исследуемого вмешательства как эквивалентной, так и превосходящей полезности, установленной в краткосрочном КИ.
Представленные статистические модели, критерии и термины анализа выживаемости могут использоваться при разработке дизайнов КИ, направленных на оценку продолжительности времени наступления ожидаемого события и кумулятивного риска во время длительного лечения и после применения ЛС.
Формулы расчета, включающие временные параметры оценки, обеспечивают корректность процедуры определения размера выборки участников для долгосрочных клинических исследований и согласуются с принципами, рекомендуемыми Коллегией Евразийской экономической комиссии для проведения качественного исследования с надлежащей оценкой соотношения «польза–риск» применения ЛС.
Вклад авторов. Все авторы подтверждают соответствие своего авторства критериям ICMJE. Наибольший вклад распределен следующим образом: O.B. Шредер — разработка концепции, написание и редактирование текста рукописи; Д.В. Горячев — критический пересмотр текста рукописи; В.А. Меркулов — разработка концепции серии обзоров.
Authors’ contributions. All the authors confirm that they meet the ICMJE criteria for authorship. The most significant contributions were as follows. Olga V. Shreder conceptualised the study, drafted and edited the manuscript. Dmitriy V. Goryachev critically revised the manuscript. Vadim A. Merkulov expanded the study concept to a series of reviews.
1. Рекомендации Коллегии Евразийской экономической комиссии от 03.11.2020 № 19 «О Руководстве по применению принципов биостатистики в клинических исследованиях лекарственных препаратов».
2. Апостериорная (послеопытная) вероятность принятия гипотезы А при условии, что имеются данные, полученные опытным путем (событие В), например ранее наблюдаемые в пилотном испытании или из источников литературы:
Р(А|В) = Р(предположения | известные данные).
3. Априорная (доопытная) вероятность — теоретическая основа для предположения вероятности наступления условного события A из числа нескольких возможных исходов В, ранее наблюдаемых в пилотном испытании или из публикаций аналогичных исследований, позволяет оценить возможность воспроизведения подобного результата в планируемом испытании: Р(А) = Р(предположение).
4. Вероятность правдоподобия или вероятность получения определенного набора данных при условии, что какая-то из гипотез верна — вероятность наступления события B при условии имеющихся предположений A: Р(В|А) = Р(известные данные | предположения).
5. Нормализация — математическая операция, применяющаяся для приведения значений апостериорной вероятности к диапазону от 0 до 1, для этого произведение вероятности правдоподобия и априорной вероятности делят на вероятность события В согласно формуле (1): Р(В) = Р(известные данные).
6. Функция выживаемости — характеристика случайной величины, связанной с некоторым множеством событий (обозначающих смерть или выбывание по разным причинам) ко времени, которая показывает вероятность того, что событие не произойдет к определенному времени, при этом случайная величина показывает время, когда событие произошло. Часто обозначается как S(t) и определяется как вероятность наступления события до определенного момента времени t: S(t) = P(T > t).
7. Цензурированные наблюдения — наблюдения, содержащие неполную информацию о состоянии субъекта по причине его непредвиденного выбывания из исследования, на графике оценки Каплана–Мейера отмечаются знаком «+». В анализе выживаемости цензурирование может быть одно- и двусторонним (правым, левым и с обеих сторон). Для оценки разницы между группами с цензурированными данными используют несколько непараметрических критериев, например критерий Вилкоксона, F-критерий Кокса, логранговый критерий.
8. Цензурированные — пациенты, которые выбывают или исключаются из исследования до наступления события в определенном интервале наблюдения и время наступления события неизвестно на момент проведения анализа выживания (выпадающие из наблюдения), или которые остались живы на момент окончания периода наблюдения.
9. Оценка максимального правдоподобия (MLE) — метод оценки параметров предполагаемого распределения вероятностей с учетом некоторых наблюдаемых данных. С точки зрения байесовского подхода MLE обычно эквивалентен максимальной апостериорной оценке P(В|А) с априорным распределением, которое является равномерным в интересующей области. В частотном подходе MLE является частным случаем экстремальной оценки, где целевой функцией является вероятность, и байесовская оценка совпадает с оценкой максимального правдоподобия P(В|А) для равномерного априорного распределения (1), где P(А|В) может рассматриваться как оценка с помощью апостериорного максимума.
10. Бета-распределение — вероятностное распределение, описывающее случайную величину, ограниченную на интервале от 0 до 1.
11. Распределение Пуассона — дискретное распределение вероятностей, которое выражает вероятность заданного числа событий, происходящих в фиксированном интервале времени. Интенсивность событий в фиксированном интервале времени обозначают λ.
12. Рекурсивное уравнение (или рекуррентное уравнение) — линейное уравнение из последовательностей, где последовательности коэффициентов могут быть представлены в виде многочленов (или линейные рекуррентные соотношения, или линейные разностные уравнения с полиномиальными коэффициентами). Рекурсивное уравнение основывается на теории рекурсивных функций и имеет вид: an = f (n, an–1, an–2, …, an–p), где an — каждый член последовательности через р предыдущих членов, n — номер члена последовательности.
13. Монотонное преобразование — процедура, производимая над некоторой упорядоченной совокупностью чисел таким образом, чтобы порядок их не изменился, например методом умножения или деления каждого из них на одно и то же число, возведение в степень, извлечение корня. Основано на правилах монотонной функции f(x), которая может быть либо возрастающей на некотором промежутке, либо убывающей: если x2>x1 и f(x2)>f(x1) — возрастающая монотонная функция, а если x2> xi и f(x2)< f(x1) — убывающая монотонная функция.
Список литературы
1. Шредер ОВ, Горячев ДВ, Меркулов ВА. Основные принципы расчета необходимой численности участников клинических исследований. Часть 1. Общие подходы (обзор). Регуляторные исследования и экспертиза лекарственных средств. 2024;14(3):338–50. https://doi.org/10.30895/1991-2919-2024-14-3-338-350
2. Thabane L. Sample size determination in clinical trials. HRM-733 Class Notes. Hamilton: St. Joseph’s Healthcare; 2004.
3. Matthews JN. An introduction to randomized controlled clinical trials. New York: Chapman & Hall; 2006. https://doi.org/10.1201/9781420011302
4. Lindley DV. A statistical paradox. Biometrika. 1957;44:187–92. https://doi.org/10.1093/biomet/44.1-2.187
5. Gittins J, Pezeshk H. A behavioral Bayes method for determining the size of a clinical trial. Ther Innov Regul Sci. 2000;34:355–63. https://doi.org/10.1177/009286150003400204
6. Gittins J, Pezeshk H. How large should a clinical trial be? J R Stat Soc Ser D Stat. 2000;49(2):177–87. https://doi.org/10.1111/1467-9884.00228
7. O’Hagan A, Stevens JW, Campbell MJ. Assurance in clinical trial design. Pharm Stat. 2005;4(3):187–201. https://doi.org/10.1002/pst.175
8. Шредер ОВ, Бунятян НД, Горячев ДВ, Сюбаев РД, Енгалычева ГН, Кузнецова АД, Косенко ВВ. Математическое прогнозирование эффективности лекарственных средств в доклинических исследованиях. Ведомости Научного центра экспертизы средств медицинского применения. Регуляторные исследования и экспертиза лекарственных средств. 2022;12(3):315–30. https://doi.org/10.30895/1991-2919-2022-12-3-315-330
9. Machin D, Campbell M, Fayers P, Pinol A. Sample size tables for clinical studies. Malden, MA: Blackwell Science; 2008. https://doi.org/10.1002/9781444300710.ch3
10. Chow SC, Shao J, Wang H, Lokhnygina Y. Sample size calculations in clinical research. New York: Marcel Dekker; 2017. https://doi.org/10.1080/24754269.2017.1398000
11. Gordon Lan KК, DeMets DL. Discrete sequential boundaries for clinical trials. Biometrika. 1983;70(3):659–63. https://doi.org/10.1093/biomet/70.3.659
12. O’Brien PC, Fleming TR. A multiple testing procedure for clinical trials. Biometrics. 1979;35(3):549–56. PMID: 497341
13. Pocock SJ. Group sequential methods in the design and analysis of clinical trials. Biometrika. 1977;64(2):191–9. https://doi.org/10.1093/biomet/64.2.191
14. Reboussin DM, DeMets DL, Kim K, Gordon Lan KK. Computations for group sequential boundaries using the Lan–DeMets spending function method. Control Clin Trials. 2000;21(3):190–207. https://doi.org/10.1016/S0197-2456(00)00057-X
15. Гланц С. Медико-биологическая статистика. М.: Практика; 1998.
16. Зулькарнаев АБ. Особенности анализа выживаемости на примере пациентов в «листе ожидания» трансплантации почки. Бюллетень сибирской медицины. 2019;18(2):215–22. https://doi.org/10.20538/1682-0363-2019-2-215-222
17. Мотренко АП. Оценка необходимого объема выборки пациентов при прогнозировании сердечно-сосудистых заболеваний. Машинное обучение и анализ данных. 2012;1(3):354–66. EDN: OXWKKF
18. Куликов СМ, Паровичникова ЕН, Савченко ВГ. Анализ выживаемости или событийный анализ: типовые ошибки ретроспективного метода. Клиническая онкогематология. Фундаментальные исследования и клиническая практика. 2010;3(2):176–83. EDN: MWJXMB
19. Jiang Z, Wang L, Li C, Xia J, Jia H. A practical simulation method to calculate sample size of group sequential trials for time-to-event data under exponential and Weibull distribution. PLoS One. 2012;7(9):e44013. https://doi.org/10.1371/journal.pone.0044013
20. Lachin JM, Foulkes MA. Evaluation of sample size and power for analyses of survival with allowance for nonuniform patient entry, losses to follow-up, noncompliance, and stratification. Biometrics. 1986;42(3):507–19. PMID: 3567285
21. Шулика ЮЕ. Анализ выживаемости авторитарных режимов в рентно-сырьевых экономиках: возможности и ограничения модели пропорциональных рисков. Вестник Пермского университета. Политология. 2018;12(4):122–39. https://doi.org/10.17072/2218-1067-2018-4-122-139
22. Hsieh FY, Lavori PW. Sample-size calculations for the Cox proportional hazards regression model with nonbinary covariates. Control Clin Trials. 2000;21(6):552–60. https://doi.org/10.1016/S0197-2456(00)00104-5
23. Schoenfeld DA. Sample-size formula for the proportional-hazards regression model. Biometrics. 1983;39(2):499–503. PMID: 6354290
Об авторах
О. В. ШредерРоссия
Шредер Ольга Васильевна, канд. биол. наук
Петровский б-р, д. 8, стр. 2, Москва, 127051
Д. В. Горячев
Россия
Горячев Дмитрий Владимирович, д-р мед. наук
Петровский б-р, д. 8, стр. 2, Москва, 127051
В. А. Меркулов
Россия
Меркулов Вадим Анатольевич, д-р мед. наук, проф.
Петровский б-р, д. 8, стр. 2, Москва, 127051
Рецензия
Для цитирования:
Шредер О.В., Горячев Д.В., Меркулов В.А. Основные принципы расчета необходимой численности участников клинических исследований. Часть 2. Анализ выживаемости (обзор). Регуляторные исследования и экспертиза лекарственных средств. 2025;15(1):92-104. https://doi.org/10.30895/1991-2919-2025-15-1-92-104
For citation:
Shreder O.V., Goryachev D.V., Merkulov V.A. Basic Principles for Calculating the Required Number of Participants in Clinical Trials. Part 2. Survival Analysis (Review). Regulatory Research and Medicine Evaluation. 2025;15(1):92-104. (In Russ.) https://doi.org/10.30895/1991-2919-2025-15-1-92-104



































